问题:
[单选] 设平面图形的速度瞬心为点c,该点的速度和加速度大小分别用Vc和ac表示,则()。
必有Vc=0,ac=0。有Vc=0,ac≠0。可能有Vc=0,ac=0。平面图形上各点速度和加速度的分布规律均与它绕定轴c转动的情况相同。
问题:
[单选] 如图所示的平面机构。半径为R的圆轮在水平粗糙面上滚动而不滑动,滑块B在水平槽内滑动。已知曲柄OA在图示铅直位置时的角速度为w1、角加速度为零,OA=AD=DB=DC=2R,此时圆轮的角速度用w2表示,则()。
w2=0。w2=w1。w2<w1。w2>w1。
问题:
[单选] 质量为2m,半径为R的偏心圆板可绕通过中心O的轴转动,偏心距OC=。在OC连线上的A点固结一质量为m的质点,OA=R如图示。当板以角速度w绕轴O转动时,系统动量K的大小为()。(注:C为圆板的质心)。
K=0。K=mRw。K=mRw。K=2mRw。
问题:
[单选] 质量为m1,半径为r的均质圆盘上,沿水平直径方向焊接一长为,质量为m2的均质杆AB。整个物体绕圆盘中心O以角速度w转动,该物体系统的总动量的大小为()。
问题:
[单选] 质点作匀速圆周运动,其动量有无变化?()
动量无变化。动量大小有变化,但方向不变。动量大小无变化,但方向要变化。动量大小、方向都有变化。
问题:
[单选] 质量为m,长度为的均质杆铰接于O点,A端固结一质量为m的质点如图示。当OA杆以角速度w绕O轴转动时,系统对轴O的动量矩的大小为()。
问题:
[单选] ]图中均质细圆环质量为m,半径为R,可绕环上O点并垂直于圆环平面的轴转动。已知角速度为w,顺时针转向,试求圆环对O轴的动量矩的大小及转向()
['
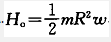
,顺时针转向。Ho=mR2w,顺时针转向。Ho=2mR2w,顺时针转向。
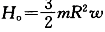
,顺时针转向。
问题:
[单选] 质点系动量对时间的一阶导数等于()。
外力的主矢。作用于质点系的所有外力的矢量和。内力的主矢。所有内力的元冲量的矢量和。
问题:
[单选] 均质细杆AB=,其B端搁置在光滑水平面上,杆由图示位置无初速地自由倒下,试分析质心C的运动()。
质心C沿曲线向右下方运动。质心C沿曲线向左下方运动。质心C沿铅直向下运动。质心C沿斜直线向右下方运动。
问题:
[单选] 长为的均质杆AD通过铰C、D与半径为的均质圆盘固结成一体如图示。设该物体系统在图示平面内对A,B,C,D各点的转动惯量分别为JA丶JB、JC、JD,则()。
JA最大。JB最大。JC最大。JD最大。
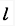 )w。
)w。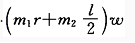 。
。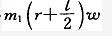 。
。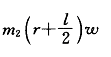 。
。
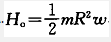 ,顺时针转向。Ho=mR2w,顺时针转向。Ho=2mR2w,顺时针转向。
,顺时针转向。Ho=mR2w,顺时针转向。Ho=2mR2w,顺时针转向。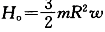 ,顺时针转向。
,顺时针转向。